|
GR9677 #41
|
|
|
|
|
Alternate Solutions |
greatm31
2008-11-07 16:52:09 | I think the problem is slightly confusing because in the question, it refers to the state of the hydrogen ATOM, and in the answers it is referring to the configuration of just the ELECTRON. The whole atom can be either in the spin singlet (s=0) or spin triplet (s=1) states. From the superscript 3=2s+1, s=1, so the state is spin triplet. But you don't need that for the answer:
If we want to write the original state of JUST THE ELECTRON, we use the given info that it's a "3p electron" so for just the electron, l=1. And the spin of JUST THE ELECTRON is s=1/2 (the spin an electron is ALWAYS 1/2). So the original configuration of the ELECTRON is:
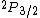
Where j=l+s for the electron. Now you can apply your selection rules and see that (A) is the only option since 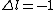 , getting you l=0 and j=l+s=1/2. , getting you l=0 and j=l+s=1/2. |  |
|
|
Comments |
gman
2010-11-10 14:29:22 | How can 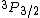 exist? doesn't that imply that S=1, L=1, and therefore |S-L| < J < S+L. Hence, J must be an integer? I don't see how J can be 3/2 given S=L=1 ... exist? doesn't that imply that S=1, L=1, and therefore |S-L| < J < S+L. Hence, J must be an integer? I don't see how J can be 3/2 given S=L=1 ...
gman
2010-11-10 15:18:56 |
I should clarify that I realize the question in awkwardly worded. The electron should have spin-1/2 and so the upper index should be a 2. But the question says it's an energy level of a hydrogen atom, which could be taken to mean the composite system of the proton+electron. Since they're both spin-1/2, the proton-electron system could have spin 0 or 1. Supposing the combined system has spin 1 and orbital angular momentum 1, we would have 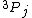 . Now I'm wondering about the lower index since j should be an integer. My question is pertinent even if we ignore the fact that this is hydrogen. It's a general question - how can this *ever* be? . Now I'm wondering about the lower index since j should be an integer. My question is pertinent even if we ignore the fact that this is hydrogen. It's a general question - how can this *ever* be?
|
|  | apr2010
2010-04-06 06:57:28 | Question to Yosun's explanation of B)
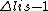 so the given reason seems to be wrong. But a dipole transition requires also $\Delta n <> 0 $ which is not fulfilled. Is that right? so the given reason seems to be wrong. But a dipole transition requires also $\Delta n <> 0 $ which is not fulfilled. Is that right?
apr2010
2010-04-06 07:06:52 |
Sorry for the typos:
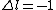 for B) for B)
but n is zero (which is not allowed).
|
|  | dcnowlin
2010-03-27 13:16:23 | Answer E is false because it is a different value of n, and is thus a different energy level, and therefore has a different energy.
p40515
2010-10-01 13:16:28 |
from where you could get that n has changed?
these states introduce only s,l,and j of the system,or one electron.
|
|  | GREview
2009-09-16 14:38:54 | This QUESTION has a TYPO in:
"A 3p electron is found in the 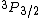 energy level of a hydrogen atom." energy level of a hydrogen atom."
Spectroscopic notation consists of: 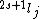 . All "energy levels" of atoms house electrons, so the multiplicity ( . All "energy levels" of atoms house electrons, so the multiplicity (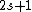 ) of an energy level is ALWAYS going to be ) of an energy level is ALWAYS going to be 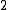 because an electron ALWAYS has because an electron ALWAYS has 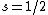 . .
The same typo is repeated in choice E, where the multiplicity is again 3.
dcnowlin
2010-03-27 13:14:14 |
Some texts include the spin of an odd nucleon in the total Russell-Saunders coupling sum of spins. I don't know why it is sometimes included and sometimes not. Perhaps that is why ETS has designated the state as S=1, because they are including the spin of the proton. The problem with this method is that all atoms would have a total integer spin, zero for even Z, and one for odd Z. Does anyone know when to include the odd nucleon and when not to in the total angular momentum? It seems that it should always be included. I don't think that electronic shielding in larger atoms would change the total angular momentum.
|
dcnowlin
2010-03-29 10:27:51 |
I should have said A instead of Z , since neutrons have spin of one-half as well.
|
|  | greatm31
2008-11-07 16:52:09 | I think the problem is slightly confusing because in the question, it refers to the state of the hydrogen ATOM, and in the answers it is referring to the configuration of just the ELECTRON. The whole atom can be either in the spin singlet (s=0) or spin triplet (s=1) states. From the superscript 3=2s+1, s=1, so the state is spin triplet. But you don't need that for the answer:
If we want to write the original state of JUST THE ELECTRON, we use the given info that it's a "3p electron" so for just the electron, l=1. And the spin of JUST THE ELECTRON is s=1/2 (the spin an electron is ALWAYS 1/2). So the original configuration of the ELECTRON is:
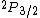
Where j=l+s for the electron. Now you can apply your selection rules and see that (A) is the only option since 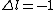 , getting you l=0 and j=l+s=1/2. , getting you l=0 and j=l+s=1/2.
maxdp
2013-09-25 21:02:41 |
"Which of the following is true about the electron in this state?"
All it say is that the electron is in a Hydrogen atom. The question itself is explicitly asking about just the electron itself.
|
|  | phys2718
2008-10-09 10:02:12 | After spending a long time checking sources on Quantum Mechanics I've decided that the superscript "3" for the spectroscopic notation in the statement of the problem is a typo or a mistake. The single electron in Hydrogen has spin s = 1/2, so this number has to be a 2, period.
DDO
2008-10-29 16:49:12 |
Moreover this implies that the spin of the electron changes during the transition (since answer A has a different total spin than the initial state and there is only 1 electron), this is not allowed for an electric dipole transition. 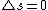
|
|  | georgi
2007-08-30 21:55:33 | delta m should also be -1. recall that the total angular momentum orbital number changed from 3/2 to 1/2. Also, the total orbital number l changed from 1 to 0 since m = -l, -l+1, ...l m =0 as well. thus it switched from m=1 to m=0 making a transition of delta m = -1 |  | physicsanator
2007-04-12 14:20:16 | The spectroscopic notation is for the top left number, the multiplicity, equal to 2s+1, for the bottom right number, the total angular momentum, J. The letter in the middle, is simply your orbital angular momentum, corresponding to your orbitals, s (l=0) p(l=1) d(l=2) and so forth.
m, the magnetic quantum number, ranges in values from -l to +l, so for each letter in the middle you have different m values. |  | hamood
2007-04-09 18:48:12 | I am confused about this, I thought the notation was rn^2s+1 L _jrnwont that mean that 2s+1 =3, meaning s =1 for this case..but shouldnt an electron have an s of 1/2...also how do we get the delta m value from the notation?
georgi
2007-08-30 21:58:18 |
the S in 2s+1 is the sum of all the 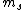 of which the electron has of which the electron has 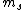 =1/2. The total spin quantum number is not necessarily 1/2 for an electron and depends on the system. delta m is obtained from the fact that we know j = =1/2. The total spin quantum number is not necessarily 1/2 for an electron and depends on the system. delta m is obtained from the fact that we know j = 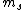 + + 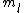 . In our case delta m is talking about the . In our case delta m is talking about the 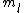 value, which changes from 1 to 0. hope this helps. value, which changes from 1 to 0. hope this helps.
|
|  | cyberdeathreaper
2007-01-15 19:48:07 | Those wondering how to decipher the notation in the question should check out the article on wikipedia for "term symbol"
FortranMan
2008-08-16 12:44:01 |
Hund's Rules is a better place to start. Also note that J=|L - S| when a shell is no more than half filled and J=L + S when the shell is over half filled.
|
|  | yubs
2006-10-29 21:40:11 | Can anyone direct me to a good explanation of the full spetroscopic notation and how it relates to the selection rules?
More specifically, what part of this notation denotes m, the magnetic quantum number? |  |
|
| Post A Comment! |
You are replying to:
I think the problem is slightly confusing because in the question, it refers to the state of the hydrogen ATOM, and in the answers it is referring to the configuration of just the ELECTRON. The whole atom can be either in the spin singlet (s=0) or spin triplet (s=1) states. From the superscript 3=2s+1, s=1, so the state is spin triplet. But you don't need that for the answer:
If we want to write the original state of JUST THE ELECTRON, we use the given info that it's a "3p electron" so for just the electron, l=1. And the spin of JUST THE ELECTRON is s=1/2 (the spin an electron is ALWAYS 1/2). So the original configuration of the ELECTRON is:
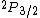
Where j=l+s for the electron. Now you can apply your selection rules and see that (A) is the only option since 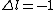 , getting you l=0 and j=l+s=1/2. |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
