|
GR9677 #52
|
|
|
|
|
Alternate Solutions |
raklaksh
2013-10-15 06:40:19 | There is a direct method to find 'l' and 'm' for a given wavefunction/spherical harmonic.
Refer D.Griffiths(Introduction to Quantum Mechanics) Eq 4.17 and Eq 4.20. |  |
|
|
Comments |
digitalhikes
2019-07-08 11:05:28 | Your article is astonishing and your article has for every condition of the mammoth substance with a good digital marketing training institute in Delhi with lighting up info. Tolerantly do not stop you earth shattering substance structure keeps it up.\r\n |  | Awardr
2017-09-14 20:39:07 | This may not be totally correct, but the geometry of the wave function reminded me of the n=2, l=1 state of the hydrogen atom. Not being symmetric along the z axis, m != 0 so m is -1 or 1, as in -h or h |  | ngendler
2015-10-23 03:37:10 | You can also just immediately eliminate (A) (Lz isn\'t gonna be 0), and (C) and (D) since l comes in steps of 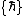 . From there, you can just guess or use the methods described in other comments. . From there, you can just guess or use the methods described in other comments. |  | nachi182
2014-09-23 13:45:38 | Here is a pretty simple solution though it requires some knowledge about quantum numbers and spherical harmonics...first of all, Lz will not give you have integers, thus B is out
When l = 0, the spherical harmonics are just some constant (duh, no angular dependence)
When m = 0, spherical harmonics will have no phi dependence. (duh, m=0, so the only angular component will come from l/theta)
From this, you can already determine that the only choices left are C and D. So either m=+/-1 or +/-2. But how do we know? well it all depends on l
In spherical harmonics, l effects theta. But looking at the theta term you can determine what l is. In this case, we have one trig function. Thus l = 1.
If l =2, we would have a 2nd trig function of theta (either cos*sin or sin^2). If l=3 we would have 3 trig functions of theta (either cos^3, or some combo of sin/cos). If you look at list of spherical harmonics you will notice that in it's most factored form, this statement holds.
There is probably a more mathematical way of what I am saying but hopefully you guys get it.
One trig function dependent of theta in our spherical harmonics, thus l = 1. Thus m can equal -1,0,1. We have a phi dependence thus m cannot equal zero. The only choice is C
dipanshugupta
2017-03-29 12:28:54 |
Really good answer. Thank you!
|
deneb
2018-10-17 23:26:06 |
Just to add on how to figure out m, here\'s what i came up with after:\r\n\r\nIn Griffith\'s QM book, he gives a generalized equation of normalized spherical harmonics (too messy to type out here). In it you\'ll realize the only phi dependent term is e^i*m*phi, so whatever is in front of the phi is equal to m. In this case m=1. If it was sin(2*phi), m would be 2. \r\n\r\nThoughts?
|
|  | raklaksh
2013-10-15 06:40:19 | There is a direct method to find 'l' and 'm' for a given wavefunction/spherical harmonic.
Refer D.Griffiths(Introduction to Quantum Mechanics) Eq 4.17 and Eq 4.20. |  | CarlBrannen
2010-10-07 15:32:46 | Given our wave function, we wish to know which z-component angular momentum 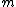 it can contain. To do this, we need to know if it can contain. To do this, we need to know if  for all possible values of for all possible values of 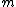 . .
You are probably expected to know that 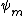 is proportional to is proportional to  = \cos(m\phi) + i\sin(m\phi)) . So we need to know if . So we need to know if
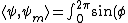 (\cos(m\phi) + i\sin(m \phi) ) d\phi = 0) . .
For 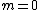 you are integrating a single copy of you are integrating a single copy of ) and get zero. This eliminates (A) and (E). For and get zero. This eliminates (A) and (E). For 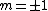 the integrals include the integrals include 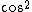 or or 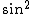 and so is non zero. The answer is therefore (C). and so is non zero. The answer is therefore (C).
Note: You already know that ) form a complete set of orthogonal functions corresponding to angular momentum in the z direction. These are linear superpositions of the two sets form a complete set of orthogonal functions corresponding to angular momentum in the z direction. These are linear superpositions of the two sets ) and and ) , other than the trivial sine when m is zero. Therefore , other than the trivial sine when m is zero. Therefore
\cos(m\phi)) and and
\sin(m\phi)) and and
\cos(m\phi)) and and
\sin(m\phi)) are non zero only for are non zero only for 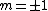 , and even when , and even when 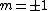 are zero unless you're looking at are zero unless you're looking at 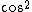 and and 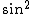 . It's also useful to know that the average values of . It's also useful to know that the average values of 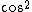 and and 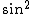 are 1/2. are 1/2. |  | WoolfianOperator
2009-11-05 19:11:27 | i think im losing it. im trying to find the expectation value of 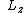 . . 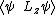 . Using . Using 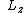 =-i =-i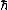 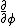 . applying the operator to . applying the operator to 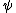 one gets a cos( one gets a cos(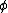 ) term. But then one has an integral from 0 to 2pi of sin( ) term. But then one has an integral from 0 to 2pi of sin(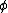 )*cos )*cos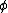 ), which is zero. I understand the other method, but why is this not appear to work? ), which is zero. I understand the other method, but why is this not appear to work?
WoolfianOperator
2009-11-06 15:31:48 |
ok. so the problem wants to know the possible outcomes. What i calculated above is the expectation value, which is the average of the possible outcomes. In order to find the possible outcomes we are really going to find the eigenvalues of the 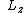 operator. One can do this using Yosun's method which involves Eulers formula. I guess my point is that one should remember that the expectation value and eigenvalues are not the same thing. operator. One can do this using Yosun's method which involves Eulers formula. I guess my point is that one should remember that the expectation value and eigenvalues are not the same thing.
|
maxdp
2013-09-26 09:38:07 |
Ahh thank you. I was wondering the same thing.
Expectation values =/= possible values. Good to remember.
|
|  | wittensdog
2009-11-03 19:53:17 | The more I think about this problem, the more I'm convinced that Void is getting at what ETS is looking for. For spherical harmonics, all of the phi dependence comes in the form of Fourier modes exp(i * m * phi). So if you can break a state down into its Fourier decomposition in phi, you can immediately read off what the values of m are. This is pretty easy to do with sin ( phi ), since you can just use Euler's formula. It would also work very easily for something like sin ( 2 * phi ), in which case you would have m = +/- 2. |  | sullx
2009-11-03 18:44:16 | Why is it that the given rigid rotator state is not even included in the above solution(s)?
One could just apply the Lz operator to the given function and equate it with the function multiplied by its eigenvalue m*h-bar.
This results in m depending on sin(PHI) which is a superposition of TWO complex functions (see the last line of void's explination below). |  | tin2019
2007-10-18 07:50:16 | Well I solved it this way: Apply the z-component operator twice to the given function 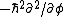 . Now this is obviously not an eigenfunction of the z component, but a superposition of two such functions. Nonetheless it is an eigenfunction of . Now this is obviously not an eigenfunction of the z component, but a superposition of two such functions. Nonetheless it is an eigenfunction of 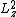 operator which yields that operator which yields that 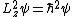 and nothing else. Square root will give correct answers (although I think that strictly speaking this is not entirely justified). and nothing else. Square root will give correct answers (although I think that strictly speaking this is not entirely justified).
syreen
2013-10-16 11:48:41 |
I don't know if this is right, but I like it!
|
|  | yosun
2005-11-10 11:40:22 | void: surround your LaTeX commands with  ... not \[slash-brackets]\... i only programmed the parser to recognize $ signs---as the LaTeX Rosetta Stone below explains. (your message has been manually re-parsed. but, use $ signs in the future!) ... not \[slash-brackets]\... i only programmed the parser to recognize $ signs---as the LaTeX Rosetta Stone below explains. (your message has been manually re-parsed. but, use $ signs in the future!)
|  | Void
2005-11-10 06:41:12 |
Let's say you forget the first few spherical harmonics. (Happens to the best of us.) Hopefully you could remember that:
1) The eigenstates of the z-component of angular momentum are given by
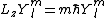
2) You'd remember the form of the angular momentum operator in the z-direction as well:
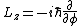
3) Combining the two, you see that the part of the spherical harmonics that contains m (besides the normalization) is proportional to 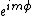 . I think this is pretty easy and important to memorize. . I think this is pretty easy and important to memorize.
The trick here is to realize in the given wave function, the information about m is contained in the 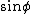 term. Ignore the others. Then remember back from complex analysis that term. Ignore the others. Then remember back from complex analysis that
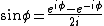 Thus, the wave function is in a superposition of states m = 1 and m = -1. The answer is C. Thus, the wave function is in a superposition of states m = 1 and m = -1. The answer is C.
testtest
2010-11-09 21:30:09 |
Definitely the best way to do it. Just try to think of which of the terms is an eigenfunction of the 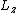 operator, and you really should start thinking about the trig identity immediately. operator, and you really should start thinking about the trig identity immediately.
|
Baharmajorana
2014-09-15 00:34:59 |
Yes I agree with u, thanks for ur best sulotion
|
ryanm
2018-10-23 02:56:31 |
This is the solution that I used and it worked. It is simple because it is easy to take the derivative.
|
|  | Void
2005-11-10 06:19:29 | |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
