|
GR9677 #56
|
|
|
|
|
Alternate Solutions |
calcuttj
2014-09-20 06:48:40 | 1/1.33 -> 3/4 -> (3/2)/2 -> 1.5/2
sin(45) = 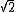 /2, /2, 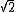 is about 1.4 is about 1.4
so our angle is slightly above 45 |  | tensorwhat
2009-04-03 07:42:49 | Easier way to think about this using critical angles for total internal reflection......
For a piece of plastic or glass with 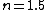 you have a critical angle of you have a critical angle of 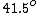 (look it up), so by decreasing the index of refraction (eg. water 1.33) you would slightly increase the critical angle so there about (look it up), so by decreasing the index of refraction (eg. water 1.33) you would slightly increase the critical angle so there about 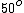
ramparts
2009-11-03 18:06:23 |
Yeah. I'll be sure to look that one up on the test. Thanks a lot.
|
|  |
|
|
Comments |
calcuttj
2014-09-20 06:48:40 | 1/1.33 -> 3/4 -> (3/2)/2 -> 1.5/2
sin(45) = 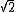 /2, /2, 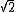 is about 1.4 is about 1.4
so our angle is slightly above 45 |  | walczyk
2012-09-29 21:53:57 | Just figured out a good approximate expansion people might want to memorize, arcsin in degrees: arcsin(z) ~ 60z + 10z^3, you get about 49.2 for this answer. You just have to be quick with your fractions. |  | mistaj
2011-08-25 11:19:41 | This is Brewster's Law: 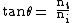 where t is the transmission medium (air n = 1.00) and i is the incident medium (water n = 1.33). Dividing 1 by 1.33, you get about 0.7. Now, where t is the transmission medium (air n = 1.00) and i is the incident medium (water n = 1.33). Dividing 1 by 1.33, you get about 0.7. Now, 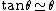 (which is really good for this problem). So, in radians we have (which is really good for this problem). So, in radians we have 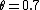 . Now, we can get an idea of this in terms of . Now, we can get an idea of this in terms of  by solving by solving 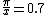 for for  which is roughly which is roughly 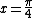 which is roughly half of 90 degrees. Choice C is the only option. which is roughly half of 90 degrees. Choice C is the only option.
mistaj
2011-08-25 11:38:57 |
Woops, misunderstood this. It still works though! But forget Brewster's Law and use sin instead of tan.
|
|  | walczyk
2011-02-25 16:42:21 | so here's how i figured out the hard part, arcsin(1/1.33): 1/1.33 is close to 3/4 (remember the inverse is 1.33!!) . sin(45) is 1/sqrt(2) so its bigger than 45 degrees (sqrt(2) is like 1.414.. so its bigger than 1.33!!) now sin(60) is sqrt(3)/2, which is like .8 or something so its less than 60 degrees. the only option left is 50 degrees, and we're done. the first time i did it i used the fact that (sqrt(3)/2)^2 is 3/4 so its obviously greater than 3/4. |  | torturedbabycow
2010-03-27 19:54:37 | As far as solving that annoying inverse sine, I think the easiest way by far is to just draw out the triangle - one side is 1, and the hypotenuse is 1.33. So, since 1.33 is pretty close to 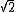 , the angle should be pretty close to 45 degrees. Stare at the triangle a few more seconds, and it becomes obvious (at least to me) that it should be a little more than 45, so voila, answer (C)! , the angle should be pretty close to 45 degrees. Stare at the triangle a few more seconds, and it becomes obvious (at least to me) that it should be a little more than 45, so voila, answer (C)! |  | jmason86
2009-10-01 19:33:10 | This is probably one to just have memorized. Stupid ETS trying to make us solve that inverse sign of 1/1.33. I hate 'em.
lrichey
2011-11-04 17:40:57 |
I agree... but here is a way I figured out....
1.33~1 1/3, hence 4/3
1/(4/3)=3/4. 3/4 is the square of a 30-60-90 triangle relation, giving inversesine(3/4)~ 60.
Which is closer to 50 degrees than 75 degrees
don't know if this works or helps at all
|
|  | f4hy
2009-04-03 17:32:47 | I only got this one because I remembered doing this exact problem in an optics class and knew that for water the angle is 50 degrees |  | tensorwhat
2009-04-03 07:42:49 | Easier way to think about this using critical angles for total internal reflection......
For a piece of plastic or glass with 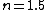 you have a critical angle of you have a critical angle of 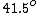 (look it up), so by decreasing the index of refraction (eg. water 1.33) you would slightly increase the critical angle so there about (look it up), so by decreasing the index of refraction (eg. water 1.33) you would slightly increase the critical angle so there about 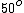
ramparts
2009-11-03 18:06:23 |
Yeah. I'll be sure to look that one up on the test. Thanks a lot.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
