|
GR9677 #60
|
|
|
Problem
|
|
|
This problem is still being typed. |
Wave Phenomena }Light Doppler Shift }Light Doppler Shift
One can derive the Doppler Shift for light as follows:
For source/observer moving towards each other, one has the wavelength emitted from the source decreasing, thus 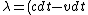 = (c - v) t_0\gamma) . Thus, . Thus, 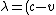\gamma\lambda_0/c) . .
For source/observer moving away from each other, one has the wavelength emitted from the source increasing, thus 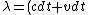=(c + v) t_0\gamma ) . Thus, . Thus, 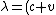\gamma\lambda_0/c) . .
Where in the last equality in the above, one applies time dilation from special relativity, 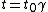 and the fact that and the fact that 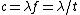 in general. in general.
Now that one has the proper battle equipment, one can proceed with the problem.
This problem is essentially the difference in wavelengths seen from a red shift and blue shift, i.e., light moving towards and away from the observer.
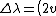\gamma\lambda_0/c \Rightarrow v = \frac{\Delta \lambda c}{2 \gamma \lambda_0} \approx \frac{\Delta \lambda c}{2 \lambda_0} \approx \frac{1.8E-12 \times 3E8}{244 E-9}\approx 2E3) , where the approximation , where the approximation 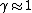 is made since one assumes the particle is moving at a non-relativistic speed. is made since one assumes the particle is moving at a non-relativistic speed.
2 km is closest to choice (B).
|
|
|
Alternate Solutions |
rizkibizniz
2012-02-25 19:08:28 | just elaborating on, and correcting @nitin's answer. Since we know the sun speed is much less than c, we use the nonrelativistic doppler effect:
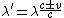
and
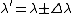
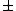 depending if its going towards (-) or away (+) the observer. depending if its going towards (-) or away (+) the observer.
since the difference is taken when the particle is at oppostite ends,
-(\lambda-\Delta\lambda) = 1.8e-12) m m
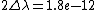 m m
so to solve this correctly, not just correct order, we must take 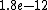 m as twice m as twice 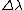 . so: . so:
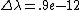 m m
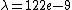 m m
plug them in to the equation
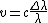
we get 2.2 km/s (B)
|  | peglegjeff
2009-10-09 16:24:44 | I thought up a different approach that simplifies things, while still using the relativistic doppler.
The two sources a at opposite sides of the sun on the equator - one is moving towards you at V, one away at V.
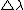 = = 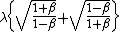
Combining under a common denominator and dividing by 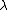 , ,
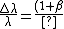-(1-\beta)}{\sqrt{(1-\beta)(1+\beta)}}=\frac{2\beta}{\sqrt{1-\beta^2}})
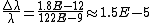 so by inspection so by inspection 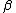 << 1, and << 1, and 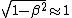
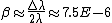
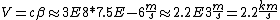
Thus B is correct. |  |
|
|
Comments |
qazx
2016-03-12 12:49:56 | you must not forget that you can call the customer care number of flipkart.com at http://thedailyburp.com/flipkart-com-toll-free-contact-helpline/ for any inconvenience. |  | rizkibizniz
2012-02-25 19:08:28 | just elaborating on, and correcting @nitin's answer. Since we know the sun speed is much less than c, we use the nonrelativistic doppler effect:
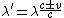
and
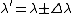
 depending if its going towards (-) or away (+) the observer. depending if its going towards (-) or away (+) the observer.
since the difference is taken when the particle is at oppostite ends,
-(\lambda-\Delta\lambda) = 1.8e-12) m m
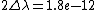 m m
so to solve this correctly, not just correct order, we must take 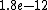 m as twice m as twice 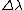 . so: . so:
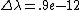 m m
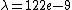 m m
plug them in to the equation
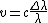
we get 2.2 km/s (B)
|  | faith
2010-11-11 19:47:29 | i got lucky and guessed that speed is very much lesser than c. and also the fact that, heck i'm not gonna let ets eat up my time.
hence the formula (from halliday)
v= (| delta lamda|/ Lamda) c
i divide it by two to average it out.
and arrived at the same answer, B. again i got lucky.
|  | wittensdog
2009-11-04 12:55:56 | Just to expand on what nitin said, if you look at the answer choices, the fastest answer, 2200 km/s, is still more than 100 times less than c. All of the answer choices are separated by powers of ten, and at 100 times less than c, there's no way we're seeing effects that big. So we're definitely pretty safely in the non-relativistic range here. So using the non-relativistic version of the formula seems like a very good idea. In general, whenever you have a problem where it looks like relativity may be involved, I would always examine the characteristic speeds in the problem. If they're something like 100 times less than c, and the answer choices have some reasonable spacing between them, I would toss the relativistic version of the formula in the interest of time.
If you don't remember the non-relativistic version, you can always get it by taking the relativistic version and throwing out terms of the form (v/c) ^ 2. |  | istezamer
2009-11-04 05:10:23 | I got this question right in less than 5 seconds !!
First of all I knew that this is ONLY a trick question!! And the trick is in changing the answer that you will get from m/sec to km/sec.. The only number that can be changed into km/s and is listed in the choices given is (E) 2200 so if we changed it to km/s it yields 2.2 k/m .. Choice (B)
istezamer
2009-11-04 05:26:40 |
Oh of course noting that the particle at the sun moves with a relatively high velocity more than 0.22 km/sec.
Although it is completely non scientific approach!! but i hate to see a question that takes that long time in solving and i still have 99 more questions to solve!!
|
wittensdog
2009-11-04 12:43:43 |
It took me a minute to realize what you were saying, but this is very clever. I guess it relies on the assumption that ETS will always try to trick people. Then again I guess that's a pretty solid bet.
|
Barney
2012-11-06 10:32:04 |
you could forget to change 220 m/s into 0.22 km/s just as well... not a reliable solution.
|
|  | jmason86
2009-10-09 18:11:14 | I guess I'm just lucky in that I've been doing solar physics research for the last 2 years.. I look at data of the sun all the time and we frequently have to correct for the differential rotation. So if you had all that under your belt.. it would be easy to see that answers (A) (D) and (E) were all absurd. The sun takes 27 days (on average) to rotate and it has a pretty large radius... so something on the order of 2km/s is reasonable. |  | peglegjeff
2009-10-09 16:24:44 | I thought up a different approach that simplifies things, while still using the relativistic doppler.
The two sources a at opposite sides of the sun on the equator - one is moving towards you at V, one away at V.
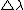 = = 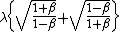
Combining under a common denominator and dividing by 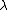 , ,
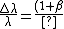-(1-\beta)}{\sqrt{(1-\beta)(1+\beta)}}=\frac{2\beta}{\sqrt{1-\beta^2}})
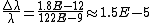 so by inspection so by inspection 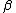 << 1, and << 1, and 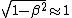
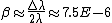
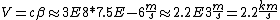
Thus B is correct.
niux
2009-11-05 13:25:35 |
did you mean a minus sign instead of summing? when initially stating delta(lambda)=.....
|
shak
2010-08-16 14:11:06 |
Thank you very much! this one is the easiest approach:)
|
faith
2010-10-17 00:40:26 |
a lil'r typo on 1st equation. its, i think, to be a subtraction of the two wavelengths. which was immediately corrected at the 2nd line. otherwise, a thorough solution.
|
maryami
2011-04-03 06:06:11 |
Thanks alot, I got confused by Yuson's soloution(I thank Yoson too for its helpful site),it is a complete and understandable one!
|
maryami
2011-04-03 06:08:48 |
Thanks alot, I got confused by Yuson's soloution(I thank Yoson too for its helpful site),it is a complete and understandable one!
|
maryami
2011-04-03 06:14:02 |
Thanks alot, I got confused by Yuson's soloution(I thank Yoson too for its helpful site),it is a complete and understandable one!
|
|  | dstahlke
2009-10-09 11:13:24 | There is one last stupid trick to this problem. I computed the answer in meters but the problem wants the answer in kilometers. Perhaps that is why only 9% of the people got this right, making it the second hardest question on the test. It's just something to keep your eye on. |  | dirichlet
2006-11-15 08:17:53 | I think there is a mistake in using \gamma
that should be 1/\gamma in formulating the shift as suggested by S.T.R. Though it doesnot affect the result as the velocity of sun along the equator gets small compared to that of light both \gamma and 1/\gamma approach the factor 1.
dirichlet
2006-11-15 08:29:25 |
Sorry, Iwas wrong , that was correct.
|
|  | nitin
2006-11-02 21:26:26 | Use the nonrelativistic Doppler shift formula instead
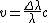 , ,
where  is the speed of the particle. In this case, is the speed of the particle. In this case,
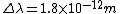 , ,
globalphysics
2006-11-03 17:32:52 |
Great simple way of getting the answer. With that approach it takes about 10 second!
|
welshmj
2007-07-31 20:42:40 |
This method gives an answer that is off by a factor of 1/2, however it gives the correct order which is really what is important.
|
theodiggers
2007-10-18 01:43:39 |
Funny, but derivation from the non-relativistic doppler shift formula correctly gives the 1/2 factor. Still, I didn't think to express it in such a compact form, rock on.
|
Shtego
2007-10-29 19:43:16 |
the change in lambda given is difference between source coming towards and going away. I suspect the change in lambda written in the non-relavistic doppler shift formula is between a source moving and as if the source were not moving. So, cut the given change in lambda by half, and now you've got the missing half factor.
|
hisperati
2007-10-31 23:34:03 |
All wrong... The 1/2 comes from the question. Read it. Your calculating the difference in velocity of the different sides of the sun, but the sun is only rotating at half that speed. Further you must subtract unity from the right side of that equation nitin has there. But the real problem is doing the arithmetic. In fact the arithmetic is so hellish, only 9% of the people takin this exam get this question right.
|
engageengage
2009-01-05 14:30:21 |
Actually the relativistic equation turns out to simplify to this once you work through all the algebrarnrnrn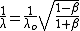 rnrnYou then have to subtract rnrnYou then have to subtract 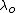 rnrn from this to get delta lambda on the left, and then simplify all of it. You end up getting:rnrn rnrn from this to get delta lambda on the left, and then simplify all of it. You end up getting:rnrn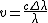 rnrnand then you have to remember to take half of the speed since, as already mentioned, the velocity is actually half since you are comparing the shifts from opposite ends of the planet, which effectively gives you double the shift.rnthat might just be a good one to memorize rnrnand then you have to remember to take half of the speed since, as already mentioned, the velocity is actually half since you are comparing the shifts from opposite ends of the planet, which effectively gives you double the shift.rnthat might just be a good one to memorize
|
engageengage
2009-01-05 14:33:55 |
adding onto my earlier comment, to get that same result, you have to throw away second order powers of 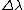 , which are tiny anyways. , which are tiny anyways.
|
niux
2009-11-05 13:33:00 |
Hisperati is right, sun speed is half of that. And if you want a similar but more accurate approach than nitin (very nice i have to admit), then start from the expression that plegegjeff gets. It is the same used by nitin but counts for the 2 factor.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
