|
GR9677 #66
|
|
|
|
|
Alternate Solutions |
The_Duck
2010-07-05 15:22:56 | Others have posted this in a more complicated way, but here's a very simple way to think about it:
Take Jupiter's orbit to be circular. Then the virial theorem says that the ratio of the magnitude of its kinetic and (negative) potential energy is 1:2. The spacecraft is going at 1.5 times Jupiter's speed so its ratio is 1.5^2:2 = 2.25:2. Since it has more kinetic than (negative) potential energy is not bound: it will escape the solar system and is thus in a hyperbolic orbit.
If you remember all of this, the trickiest part is remembering to square 1.5. The virial theorem is very nice to know here; it lets you avoid mucking around with any sort of explicit potential, real or effective. |  | GREview
2009-09-18 00:14:03 | The spacecraft is "on a mission to the outer planets" so why would be in an orbit that doesn't allow it to escape? Thus it's either D or E. Given that D is a very special case, one chooses E. |  | apps
2009-08-08 05:57:11 | I believe it could be solved in a simpler way.
We know that Jupiter orbits around the Sun and doesn't fall. So its speed is at least V_c=$\sqrt{GM/R}.
One should have kinetic energy equals or greater than potential energy of gravitational field in order to leave the Sun:
mV^2/2 >= GmM/R
V >= $\sqrt{2*GM/R} >= $\sqrt{2} * V_c ("=" means parabola)
1.5 > $\sqrt{2} means that spacecraft has sufficient energy to leave |  | OrbitGirl
2007-10-02 10:39:35 | It doesn't have to be that complicated.
One could just recognize that an object traveling at 1.5 times the speed of Jupiter in the same vicinity would be traveling in excess of escape velocity with respect to the Sun. Speed greater than escape velocity results in a hyperbolic orbit. QED.
You can check with NASA if you don't believe me: http://www.hq.nasa.gov/office/pao/History/conghand/traject.htm
Blue Quark
2007-10-27 17:24:23 |
The trouble is finding the escape velocity. The easiest way is to recognize that the acceleration needed for circular orbits is centripetal acceleration equal to a=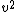 /r /r
Then ma=G(M*m)/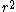  m m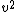 /r=G(M*m)/ /r=G(M*m)/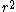
Solve and find 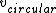 = =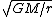
To find escape velocity, set kinetic energy equal to gravitational potential energy.
1/2*m*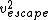 =G*(M*m)/r =G*(M*m)/r
Solve and find 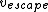 = =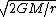
The end result is that 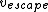 = = 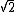 * *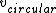
Since 1.5>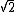 the velocity is greater than the escape velocity and hence it travels a hyperbolic path about the sun. the velocity is greater than the escape velocity and hence it travels a hyperbolic path about the sun.
|
|  | sharpstones
2007-04-05 07:29:46 | Ok, here's how to do the problem. Along with memorizing the Effective Potential you really should memorize the total energy of a body in a circular orbit:
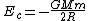
And the Virial Theorem:
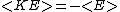
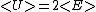
And the classification of orbits
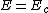 => circular orbit => circular orbit
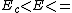 => elliptical orbits => elliptical orbits
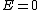 => parabolic orbit => parabolic orbit
$E > 0 $=> hyperbolic orbit
On to the problem: Since Jupiter has an elliptical orbit we know that:
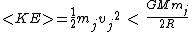
=>

Now for the spaceship you know that
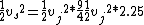
At this point the approximation you make is that Jupiter's orbit is not very far from a circle so E is close to E_c and that means that
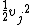 is close to is close to 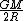
so for sure multiplying 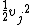 by 2.25 will make it greater then by 2.25 will make it greater then 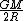 which will bring you to the hyperbolic regime which will bring you to the hyperbolic regime |  |
|
|
Comments |
fireballs
2019-09-13 14:18:36 | Here\'s an even simpler solution. You know that for an elliptical orbit, the speed of the body is: 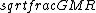 < < < < 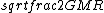 Assume for the sake of argument that Jupiter\'s velocity saturates the lower bound here, i.e. that it is a circular orbit and Assume for the sake of argument that Jupiter\'s velocity saturates the lower bound here, i.e. that it is a circular orbit and  = = 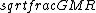 . Then the speed of the spacecraft is . Then the speed of the spacecraft is 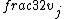 = = 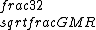 = = 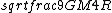 > > 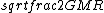 \r\n\r\nSo the orbit must be hyperbolic. \r\n\r\nSo the orbit must be hyperbolic. |  | aziza
2014-08-11 14:32:33 | I thought this was a Hohmann orbit transfer question..so I chose (c) ellipse :( |  | phoxdie
2010-11-10 16:36:46 | Very curious. In the "offical" solution it is stated that the total energy of the spacecraft is:
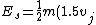^2 + V_eff)
and for Jupiter it is:
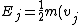^2 + V_eff)
then the claim is made that the spacecraft energy is greater than Jupiters based solely on the fact that it has a greater velocity. How can this be correct considering that the spacecraft must have a mass much much much less than that of Jupiter? Rereading what you have I noticed that the 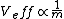 so in this case I believe the correct reasoning for the ship having a greater energy than Jupiter is because it has a much smaller mass. Since both the planet and the ship are at roughly the same distance from the Sun any so in this case I believe the correct reasoning for the ship having a greater energy than Jupiter is because it has a much smaller mass. Since both the planet and the ship are at roughly the same distance from the Sun any  dependence can be neglected. dependence can be neglected.
I don't disagree with the answer, only the way in which it is explained. |  | The_Duck
2010-07-05 15:22:56 | Others have posted this in a more complicated way, but here's a very simple way to think about it:
Take Jupiter's orbit to be circular. Then the virial theorem says that the ratio of the magnitude of its kinetic and (negative) potential energy is 1:2. The spacecraft is going at 1.5 times Jupiter's speed so its ratio is 1.5^2:2 = 2.25:2. Since it has more kinetic than (negative) potential energy is not bound: it will escape the solar system and is thus in a hyperbolic orbit.
If you remember all of this, the trickiest part is remembering to square 1.5. The virial theorem is very nice to know here; it lets you avoid mucking around with any sort of explicit potential, real or effective.
Quark
2011-10-19 14:47:25 |
I think this solution is the quickest and easiest to understand conceptually. The only set back would be recognizing when you can use the virial theorem.
|
Quark
2011-10-19 15:30:32 |
Just to make things a bit more explicit for those that are not familiar with the virial theorem. The virial theorem gives a relation between the total kinetic energy of a system to the total potential energy of that system. Mathematically,
2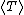 =n =n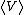
where n comes from V(r)=a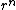 . Since the force here is just the gravitational force which is proportional to . Since the force here is just the gravitational force which is proportional to 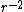 , we have that the potential is proportional to , we have that the potential is proportional to 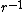 . Therefore our ratio of the kinetic energy to the potential energy for Jupiter is . Therefore our ratio of the kinetic energy to the potential energy for Jupiter is
2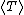 = =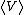
where the right-side is positive since the potential is negative and n=-1. Now if we solve for the total kinetic energy we get that
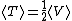
which states that the Kinetic energy is half of the potential energy and therefore Jupiter doesn't have enough kinetic energy to escape the sun's gravitational pull (hence it's orbit around the sun). Thus the ratio of the potential energy to the kinetic energy of Jupiter is 2:1 Now we want to find this ratio for the spaceship. Since the spacecraft is traveling at 1.5 times the speed of Jupiter, its 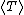 will be will be 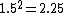 larger than that of Jupiter's since kinetic energy is proportional to larger than that of Jupiter's since kinetic energy is proportional to 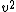 . Our new ratio of potential energy to kinetic energy is 2:1(2.25) showing that the spacecraft has more kinetic energy than potential energy and will thus escape the sun. . Our new ratio of potential energy to kinetic energy is 2:1(2.25) showing that the spacecraft has more kinetic energy than potential energy and will thus escape the sun.
|
dragore
2012-06-26 15:38:40 |
^ You seem to forget that also depends on the mass. It would be nonsense to conclude that the kinetic energy of a spaceship could be larger than that of Jupiter.
|
|  | GREview
2009-09-18 00:14:03 | The spacecraft is "on a mission to the outer planets" so why would be in an orbit that doesn't allow it to escape? Thus it's either D or E. Given that D is a very special case, one chooses E.
someone
2011-11-06 16:32:13 |
I like this solution.
|
Nebula
2015-09-16 22:12:36 |
Easily the quickest solution.
|
|  | apps
2009-08-08 05:57:11 | I believe it could be solved in a simpler way.
We know that Jupiter orbits around the Sun and doesn't fall. So its speed is at least V_c=$\sqrt{GM/R}.
One should have kinetic energy equals or greater than potential energy of gravitational field in order to leave the Sun:
mV^2/2 >= GmM/R
V >= $\sqrt{2*GM/R} >= $\sqrt{2} * V_c ("=" means parabola)
1.5 > $\sqrt{2} means that spacecraft has sufficient energy to leave
archard
2010-09-30 19:56:27 |
This is what ETS is getting at I think, and probably the best way of going about getting the right answer.
|
|  | OrbitGirl
2007-10-02 10:39:35 | It doesn't have to be that complicated.
One could just recognize that an object traveling at 1.5 times the speed of Jupiter in the same vicinity would be traveling in excess of escape velocity with respect to the Sun. Speed greater than escape velocity results in a hyperbolic orbit. QED.
You can check with NASA if you don't believe me: http://www.hq.nasa.gov/office/pao/History/conghand/traject.htm
Blue Quark
2007-10-27 17:24:23 |
The trouble is finding the escape velocity. The easiest way is to recognize that the acceleration needed for circular orbits is centripetal acceleration equal to a=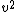 /r /r
Then ma=G(M*m)/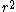  m m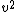 /r=G(M*m)/ /r=G(M*m)/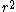
Solve and find 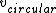 = =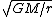
To find escape velocity, set kinetic energy equal to gravitational potential energy.
1/2*m*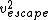 =G*(M*m)/r =G*(M*m)/r
Solve and find 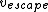 = =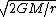
The end result is that 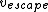 = = 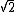 * *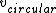
Since 1.5>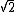 the velocity is greater than the escape velocity and hence it travels a hyperbolic path about the sun. the velocity is greater than the escape velocity and hence it travels a hyperbolic path about the sun.
|
gliese876d
2008-10-11 21:04:37 |
blue quark, that's a great way of looking at it. also, it just sort of seems logical, doesn't it, that if the spacecraft is bound for the outer planets, it probably needs a hyperbolic orbit
|
motek
2008-10-21 09:45:42 |
Blue's solution is better because it does not assume that the mass of the spacecraft is equal to the mass of Jupiter, which is wring and is assumed by the first solution
|
hanin
2009-09-29 22:10:40 |
@Blue Quark
Nice solution!
Small question: what if the speed is between circular and escape velocity? An ellipse orbit? --> that way the number 1.5 in the problem is essential
|
shak
2010-08-16 21:09:25 |
good analysis!!!!!thank u
|
flyboy621
2010-11-02 21:53:55 |
Good solution, Blue Quark. Hanin, I think your comment highlights why you have to do the calculation. If the spaceship's speed had been 1.3 times Jupiter's (less than 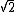 that is), it would be an elliptical orbit. that is), it would be an elliptical orbit.
|
|  | sharpstones
2007-04-05 07:29:46 | Ok, here's how to do the problem. Along with memorizing the Effective Potential you really should memorize the total energy of a body in a circular orbit:
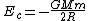
And the Virial Theorem:
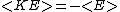
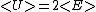
And the classification of orbits
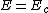 => circular orbit => circular orbit
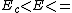 => elliptical orbits => elliptical orbits
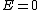 => parabolic orbit => parabolic orbit
$E > 0 $=> hyperbolic orbit
On to the problem: Since Jupiter has an elliptical orbit we know that:
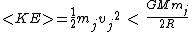
=>

Now for the spaceship you know that
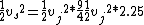
At this point the approximation you make is that Jupiter's orbit is not very far from a circle so E is close to E_c and that means that
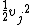 is close to is close to 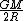
so for sure multiplying 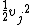 by 2.25 will make it greater then by 2.25 will make it greater then 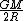 which will bring you to the hyperbolic regime which will bring you to the hyperbolic regime |  | sharpstones
2007-04-05 06:53:51 | I also don't understand this reasoning considering in the above equations for the KE the same mass is used for Jupiter and the spaceship?? |  | cyberdeathreaper
2007-01-28 11:23:56 | I think I'm not understanding something here...
In part (B) you say "the energy of Jupiter is greater than that of the spaceship"
But in part (C) you state that while the energy of Jupiter falls between Vmin and 0, the total energy of the spacecraft must be greater than 0, implying the spacecraft has more energy than Jupiter.
Both can't be true - intuition tells me Jupiter has more energy, but I'm unsure how that leads to the correct answer.
tau1777
2008-11-07 11:56:00 |
so remembering
Energy, Orbit
E > 0, hyperbola
E = 0 , parabola
Vmin < E<0 ellipse
E=Vmin, Circle
i was assuming that jupiter has ellipitical orbit, then you know its either parabola or hyperbola. but moving so fast that KE term is large to most likely hyperbola. this solution is probably un-settling as is requires a bit of luck. but once you can get it down to two choice, it pays off to take a shot.
|
|  | quarky
2005-12-09 17:19:33 | How can you know the energy of the spaceship without knowing its mass?
rawr
2009-09-25 19:51:01 |
You know that it's A LOT less massive than jupiter. that's all you need for a basic analysis
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
