|
GR9677 #80
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics }Wave Phenomena }Wave Phenomena
There's a long way to solve this problem and then a short. One looks at the choices to find the one that first the physical deduction: when 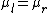 , the whole incident wave should be transmitted, with 0 reflection. Moreover, in the limit of , the whole incident wave should be transmitted, with 0 reflection. Moreover, in the limit of 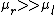 there should be 0 transmission. Choice (C) is the only one that fits this condition, leading to a ratio of 1 for there should be 0 transmission. Choice (C) is the only one that fits this condition, leading to a ratio of 1 for 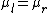 . .
One can also calculate the exact form of the transmission coefficient for this multi-density string. Take the following,
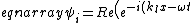} \right)\\
\psi_r = \left( Re R e^{-i(-k_l x-\omega t)} \right)\\
\psi_t = \left( Re T e^{-i(k_r x-\omega t)} \right)<br />
\end{eqnarray})
At the boundary between different density parts, one applies continuity +\psi_r(x=0)=\psi_t(x=0)) to get 1+R=T. to get 1+R=T.
One applies  - \frac{\partial \psi}{\partial x}(x>0)) , where , where 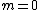 since there is no point particle situated at the origin, to obtain since there is no point particle situated at the origin, to obtain =ik_r T) . .
Recalling the nifty relation 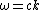 and and 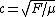 , one solves for T to get , one solves for T to get 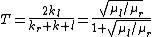 , as in choice (C). , as in choice (C).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Jon V
2015-08-09 23:34:16 | Quick solution involving limiting behavior. As 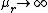 , the "rope" acts like a immovable wall and so we should expect , the "rope" acts like a immovable wall and so we should expect  , that is, no transmission. Only answer C satisfies this condition. Choose it! , that is, no transmission. Only answer C satisfies this condition. Choose it!
We can confirm this by observing also that as 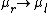 , the "rope" just becomes and extension of the string, and so we should expect , the "rope" just becomes and extension of the string, and so we should expect  , that is, no reflection. Here both B and C gives this result, but we already eliminated B earlier! , that is, no reflection. Here both B and C gives this result, but we already eliminated B earlier!
Whenever you are given symbolic answers (as oppose to numeric), try a few limiting cases to eliminate answers. Occasionally, you get lucky and the right answer just falls out!
Yifann
2023-10-16 11:57:43 |
Totally agreed, this approach is fascinating.
|
|  | Baharmajorana
2014-09-16 12:58:27 | I can't calculate this problem. But I have a knowledge of the combination of less dense and more dense string, I assumed that if miu-left>Miu-right we face a free end so we have an amplitude with more magnitude , and for reverse condition we face a rigid end then we have less magnitude.
A) totally faulse
B) violate our condition
C) exactly fulfill our condition
D) gave us minus magnitude !!!!
C) totally faulse
Hahah so easy, yeah?? |  | hooverbm
2012-11-02 09:49:15 | Actually, it is dead wrong that answer C is the only one with an amplitude less than 1.
You don't have to know much to answer this question. Do a process of elimation. Pick numbers for the mass density.
A) No, some of the wave is reflected.
B) Amplitude is larger than one. Nope.
C) Amplitude is less than one, could work.
D) Amplitude is also less than one, could work. Sign is negative.
E) Nope, part of the wave will be transmitted.
That brings you to C and D. Note, the sign is negative. The transmitted wave is upright, NOT inverted. Thus the solution must be C. |  | testtest
2010-09-20 18:45:10 | If 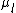 < < 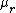 , then the amplitute must be less than 1. Only C fits. , then the amplitute must be less than 1. Only C fits. |  | apr2010
2010-04-07 04:10:06 | Limits will do the trick:
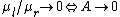
only C fullfills this.
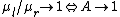
only B and C fullfill this
|  | BerkeleyEric
2010-04-06 23:35:36 | A) and E) can be eliminated immediately from physical intuition. B) and D) can then be eliminated since they do not tend to zero as 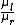 goes to zero. goes to zero. |  | schadenfraude
2008-11-02 09:28:50 | You may also notice that the correct answer should be similar to the form 2m1/(m1+m2) because this problem is analogous to an elastic collision with one particle initially at rest: the transmitted wave is analogous to the motion of the particle that was initially at rest after being hit by an incident particle. This formula has helped me about four times on this test alone, so it is probably a good one to memorize.
Kabuto Yakushi
2011-03-07 17:32:58 |
This analogy helped me too. The elastic collision formulas are also analogous to optical waves transmission as well. I agree, they are important to memorize.
|
|  | yosun
2005-11-11 22:54:35 | keflavich: good luck to u too, and to all a good night. i'm out for the night. everyone: have fun on saturday! |  | keflavich
2005-11-11 21:52:25 | Good call, thanks for the revision. Looking at limiting cases seems like a good idea in general. I hope I remember that when I'm taking the test.
Good luck to all taking it tomorrow, and Yosun, thanks for making the site. |  | yosun
2005-11-11 21:22:51 | keflavich: one can also avoid the formalism by looking at the limit of high density on the right wave. should be no transmission if so. (see revised sol'n above) |  | keflavich
2005-11-11 19:05:29 | Actually, A, B, and C all fit that 'easy' deduction, though it's pretty easy to eliminate A. I ended up having to flip a coin between b an c, since they only differe by which 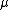 is on top. is on top.
physicsisgod
2008-10-30 15:36:04 |
B doesn't go to zero when 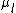 << << 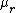
A doesn't depend on either densities at all.
Only C fits the limiting cases.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
