|
GR9677 #82
|
|
|
|
|
Alternate Solutions |
flyboy621
2010-11-05 21:49:06 | For the film to appear bright, we want the light reflected from the bottom of the upper glass (which is not phase-shifted) to be in phase with the light reflected from the top of the lower glass (which has its phase reversed upon reflection).
The path difference is 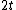 , so we have the following: , so we have the following:
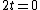 gives destructive interference (so we rule out A, B, and C) gives destructive interference (so we rule out A, B, and C)
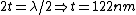 gives constructive interference gives constructive interference
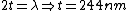 gives destructive interference again (so we rule out D) gives destructive interference again (so we rule out D)
E is left. |  |
|
|
Comments |
johnVay
2013-10-08 20:10:38 | a good way to see why there's no phase shift is to check out the drawing here:
http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/interf.html
the interface they're looking at is: glass/air/glass
imagine infinite glass on both direction and air trapped inside. incident light reflecting off the top of the air layer doesn't phase shify b/c n_glass > n_air
but the second reflection switches up because we're going from air to glass.
the mistake is to think as if we're coming from air into glass to begin with. i think they just want us to think about a glass-air-glass system.
Ryry013
2019-10-22 06:22:59 |
Fixed link: http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/interf.html
|
|  | mpdude8
2012-04-20 18:23:36 | How could a film appear bright if it has no thickness at all? Eliminate A, B, C immediately. |  | mistaj
2011-08-28 09:12:14 | More info for the current solution:
For constructive interference in a thin film with n = 1 (air) and 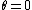 ("from above") we can use the formula ("from above") we can use the formula  = (m - 1/2)\lambda) . Thus, beginning with m = 1, 2, 3... we find . Thus, beginning with m = 1, 2, 3... we find 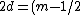\lambda) , which is simply , which is simply 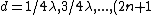/4 \lambda) for for 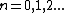 . .
neo
2011-09-11 10:00:12 |
I totally agree with this solution.
But , why we are not considering phase change due to travel in an upper glass?
|
|  | flyboy621
2010-11-05 21:49:06 | For the film to appear bright, we want the light reflected from the bottom of the upper glass (which is not phase-shifted) to be in phase with the light reflected from the top of the lower glass (which has its phase reversed upon reflection).
The path difference is 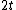 , so we have the following: , so we have the following:
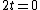 gives destructive interference (so we rule out A, B, and C) gives destructive interference (so we rule out A, B, and C)
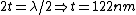 gives constructive interference gives constructive interference
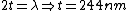 gives destructive interference again (so we rule out D) gives destructive interference again (so we rule out D)
E is left.
kaic
2013-10-15 16:55:28 |
technically the light reflected from the upper glass is reflected with its phase shifted by  , while the light reflected from the bottom will experience a second phase shift, so its total phase shift is , while the light reflected from the bottom will experience a second phase shift, so its total phase shift is 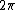 . It works out the same, but light reflecting off a medium of higher refractive index always undergoes a half-phase shift. . It works out the same, but light reflecting off a medium of higher refractive index always undergoes a half-phase shift.
|
|  | apr2010
2010-04-07 04:38:32 | Compare this question with http://grephysics.net/ans/0177/69 , where a thin oil film on glass requires
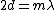 as the light changes phase from air to oil and again oil to air. In our case the light changes phase three times from air to glass, air to glass and air to glass requiring as the light changes phase from air to oil and again oil to air. In our case the light changes phase three times from air to glass, air to glass and air to glass requiring
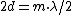
apr2010
2010-04-07 04:40:29 |
typo: air (n=1.0) to oil (n=1.2) and oil to glass (n=1.6)
|
|  | shafatmubin
2009-11-05 14:00:21 | I surmised the answer by looking at the choices - I knew that the wavelength had to be (n+1/2)LAMBDA, and not (n+1/4)LAMBDA.
Choice E was the only one that fit. |  | f4hy
2009-04-03 19:05:26 | Band filters are made by taking two glass plates and having a gap in the middle that is some half wavelength of light. So I knew C and D would have the light transmitted through. Since E would function as a band pass filter for some other wavelength of light, it would have to reflect the light we were given. So I picked E. |  | p3ace
2008-04-11 12:41:45 | Isn't the condition for contructive interference based on having the light strike the interface at a node in the wave? If this is the case then I don't see how you can have any constructive interference with the wave striking the interface at the antinode. I know that what you say is correct. I just don't understand why. |  | newton
2007-09-27 03:29:06 | The light reflected from the top glass plate and the light reflected from bottom glass plate will both undergo a phase shift of pi.
so condition for constructive interferance is
2t=m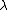 or or
t=m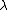 /2, where m is odd. /2, where m is odd.
newton
2007-09-27 03:55:04 |
I just wanted to edit my post. Here we should consider only reflections at the top and the bottom of the air gap. Reflections from the top of the air gap experience no phase shift while those from the bottom experience a half-cycle phase shift. Hence another half-cycle phase shift is necessary to bring the reflections into a relative phase shift of one complete cycle and lead to constructive interference.
Hence for constructive interfernce
2t=m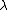 /2 /2
|
wangjj0120
2008-09-25 03:46:39 |
I don't understand.
Why should we consider only reflections at the top and the bottom of the air gap? Why not the reflections at the top of the upper glass plat and the second glass plate?
|
dstahlke
2009-10-09 12:25:11 |
wangjj0120: I think that you don't consider the top of the top plate or bottom of the bottom plate because you don't know how thick the glass is. In any case, the problem is about what goes on in the air gap. There was a problem in my E+M class that involved reflections (and double reflections, triple reflections, as the light bounces around) from multiple surfaces and it took an hour to sort them all out.
|
|  | cyberdeathreaper
2007-02-04 18:00:20 | I'm confused why you wouldn't use the formula for constructive interference in thin films:
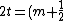\lambda_n)
With m = 0,1,2,...
and
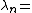
wavelength of light in a medium whose refraction index is n.
sharpstones
2007-04-01 10:18:37 |
it's all good. Set m=0 in your equation and you will get the same equation that is presented in this situation. The first transition from air to glass will reflect a wave with pi phase difference so you want the total phase change when traveling through the material and back to be equal to an odd multiple of pi.
|
|  | grep
2006-10-27 13:51:59 | Actually, only the parallel components undergo a pi phase shift at the first reflection, and then at the second reflection, only the perpendicular light components undergo a pi phase shift. (or vice versa depending on which interface has the higher n.) The net result is an overall phase shift for all components of the light of pi radians. Check out an optics reference's section on Fresnel equations if this is unclear. |  | poop
2005-12-08 08:18:54 | I\'m confused -- the light reflected at the top glass plate, and the light reflected at the bottom glass plate, BOTH undergo a phase shift by pi...shouldn\'t those cancel out to give 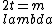 ? ?
Ethan
2008-10-08 09:46:48 |
I believe the question is worded ambiguously. If we are supposed to picture the glass plate/air setup as sitting in air itself, and the glass thickness as negligible, than the condition is indeed 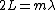 . However if we imagine the light source embedded in the glass we get . However if we imagine the light source embedded in the glass we get 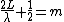 which is the "correct" answer. which is the "correct" answer.
|
Ethan
2008-10-08 09:48:22 |
I believe the question is worded ambiguously. If we are supposed to picture the glass plate/air setup as sitting in air itself, and the glass thickness as negligible, than the condition is indeed 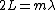 . However if we imagine the light source embedded in the glass we get . However if we imagine the light source embedded in the glass we get 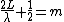 which is the "correct" answer. which is the "correct" answer.
|
archard
2010-08-06 09:00:12 |
The light only undergoes a phase shift when being reflected by a medium with higher index of refraction than the medium it comes from. Glass has a higher index of refraction than air, so the light that reflects from the Glass|Air interface does not undergo a phase shift, while the light that reflects from the Air|Glass interface does.
|
his dudeness
2010-08-12 07:17:30 |
This question is very poorly worded. Since they don't tell us the thickness of the glass, I guess we are meant to assume very thick glass plates with the light source coming from inside the glass. That is the only way their answer makes sense.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
