|
GR9677 #83
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics }Rippled Surface }Rippled Surface
The simple intuitive way to solve this is to note that for 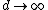 , , 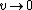 , since one gets an infinitely steep (vertical line) hill, and the only way for the particle to stay on the surface (i.e., not accelerate on it) at the vertical drop is if its velocity is 0. The onyl choice with d on the denominator is choice (D). , since one gets an infinitely steep (vertical line) hill, and the only way for the particle to stay on the surface (i.e., not accelerate on it) at the vertical drop is if its velocity is 0. The onyl choice with d on the denominator is choice (D).
The more rigorous solution is due to Sara Salha.
Equating centripetal force with gravity at the top of the hill, one has 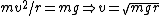 . The non-trivial bit comes from calculating the radius. . The non-trivial bit comes from calculating the radius.
Recall the radius of curvature from calculus 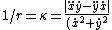^{3/2}}) . Defining a parameter t as the independent variable, and defining . Defining a parameter t as the independent variable, and defining 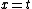 , , 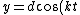) , one finds that , one finds that 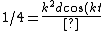}{1+(kd)^2\sin^2(kt)}) . Evaluate it at . Evaluate it at 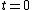 to find to find =k^2d \Rightarrow r=1/(k^2d)) , the radius of curvature at the top of the hill. Plug that into the equation for velocity above to get , the radius of curvature at the top of the hill. Plug that into the equation for velocity above to get 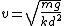 , as in choice (D). , as in choice (D).
|
|
|
Alternate Solutions |
ryanmes
2018-10-24 21:32:38 | The easiest way to look at so many problems on this exam is limits. If d increases, then you need a smaller velocity to stay on the track. There is only one answer where this is the case (when d is in the denominator). And this is the answer. |  | elxcats
2013-10-14 20:33:49 | The condition for the object to fly off is that the normal force is equal to zero. So let's set up our force equation!
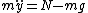
But 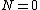
So
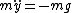
using 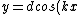)
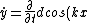)
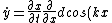)
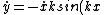)
Doing basically the same thing again to find 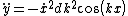)
Plugging that into the force equation we find
 = -mg)
Solving for 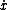
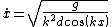}})
The question asks for the velocity which the above condition will always be met. This means you want to maximize the cosine term (1) which gives you answer (D).
Hope that gives some insight! |  | Herminso
2009-09-21 12:24:31 | Physically the limit case is such that:
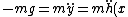) , ,
just when the particle will stay yet on the surface al all times. The particle go out of the path if |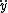 | > | | > |) |, in that case the trayectory can raising off the surface. Now, |, in that case the trayectory can raising off the surface. Now,
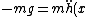=-mdk^2\dot{x}^2 \cos ^2{(kx)}=-mdk^2v_x^2\cos ^2{(kx)}) , ,
so 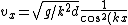}})  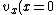=\sqrt{g/k^2d}) , and then , and then 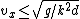 . . |  | Rus Almighty
2008-04-29 08:35:33 | A condition for the body to stay on the track:
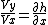
let's derive both sides by t and remember that on the top 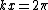 , Vx is V , , Vx is V , 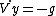 and and 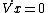 'cuase there is only gravitational force on the top. 'cuase there is only gravitational force on the top.
we get:
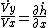
now let's calculate 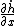
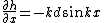
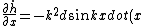 = - Vx k^2 d cos kx )
And from now on it's only algebra:
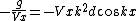
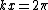
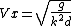
QED |  |
|
|
Comments |
ryanmes
2018-10-24 21:32:38 | The easiest way to look at so many problems on this exam is limits. If d increases, then you need a smaller velocity to stay on the track. There is only one answer where this is the case (when d is in the denominator). And this is the answer. |  | ana123
2017-09-09 03:29:16 | h\'\'(x) = g\r\n (dx^2/dt^2)) \r\n \r\n=g) \r\nv= \r\nv= }) \r\n \r\n
ana123
2017-09-09 03:41:20 |
Excuse the formatting.\r\n\r\nCorrection\r\nh\'\'(x)= g\r\n(dx^2/dt^2)) \r\n \r\n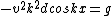 \r\n \r\n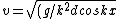})
|
|  | elxcats
2013-10-14 20:33:49 | The condition for the object to fly off is that the normal force is equal to zero. So let's set up our force equation!
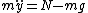
But 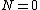
So
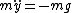
using 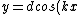)
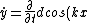)
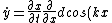)
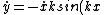)
Doing basically the same thing again to find 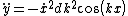)
Plugging that into the force equation we find
 = -mg)
Solving for 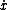
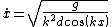}})
The question asks for the velocity which the above condition will always be met. This means you want to maximize the cosine term (1) which gives you answer (D).
Hope that gives some insight! |  | mpdude8
2012-04-20 18:26:28 | The only choices that give you the correct units of m/s for velocity are C and D.
hoboboxer
2013-04-11 18:44:03 |
Not true. Choice (A) gives units of m/s as well.
|
|  | blackhole_taw
2010-11-09 13:12:15 | 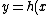 = d cos(kx))
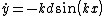 \dot{x})
![\ddot{y} = - \left[ k^{2} d cos(kx) \dot{x}^{2} + k d sin(kx) \ddot{x} \right]](/cgi-bin/mimetex.cgi?\ddot{y} = - \left[ k^{2} d cos(kx) \dot{x}^{2} + k d sin(kx) \ddot{x} \right])
put 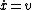 and and 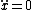 . .
extreme value for 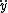 is is 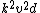 , which is eventually equal to g. , which is eventually equal to g.
thus 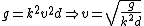 |  | Chespirito
2010-10-03 01:19:18 | Take a limit as d goes to 0: the surface is flat. The particle can then go at any horizontal speed and still touch the surface. The only answer which allows for the speed to be arbitrarily large is D.
flyboy621
2010-11-05 22:00:01 |
Nice solution.
|
|  | sullx
2009-11-04 22:50:31 | In the case that one does not realize the limiting scenario that Yosun provided, one could approximate the solution by doing some baby physics:
For a particle traveling over one of the given "ripples" consider the force equation:
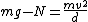
This crudely approximates the ripple as a circle with radius d. The max speed just before the particle lifts off the ripple will be when 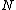  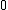 . Solving for v gives . Solving for v gives 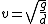 as the upper limit. as the upper limit.
Only answer D resembles this.
cilginfizikci
2010-03-08 23:42:31 |
you have solved the equation wrongly... V= (gd)^0.5... and according to ur solution the answer is A... check ur calc. pls
|
|  | Herminso
2009-09-21 12:24:31 | Physically the limit case is such that:
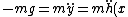) , ,
just when the particle will stay yet on the surface al all times. The particle go out of the path if |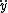 | > | | > |) |, in that case the trayectory can raising off the surface. Now, |, in that case the trayectory can raising off the surface. Now,
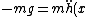=-mdk^2\dot{x}^2 \cos ^2{(kx)}=-mdk^2v_x^2\cos ^2{(kx)}) , ,
so 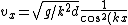}})  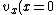=\sqrt{g/k^2d}) , and then , and then 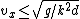 . .
wavicle
2012-08-04 17:46:58 |
tl; dr - can skip...I'm studying for the quals and using the occasional "interesting" GRE problem as a refresher. Since this "solution" is listed at the top, I had to login to clarify some things.
You will not get such a simple equation when you do )
Note
 \prop sin(kx) \dot{x})
 \prop \dot{x}^2 cos(kx) + \ddot{x} sin(kx))
I'm not trying to get the signs right, just showing that this was done incorrectly. It's much easier to work with ) for reasons seen above. for reasons seen above.
|
|  | jw111
2008-11-07 21:51:08 | draw a free projection track on question first
the trajectory is
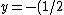g\frac{x^2}{v^2})
the condition that the particle stay on the surface is
the trajectory ALWAYS below the suface
that is at x = 0 (as you can see from your drawing)
|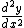 | > | | > |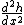 | |
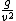 > > 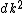
|  | ayabepaula
2008-10-23 17:24:21 | 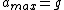
by definition
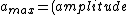\times{(\omega)^{2}})
Since
=Asin(\omega.t+\phi))
Here
Amplitude=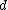
then
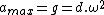
but
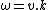
then
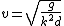
chemicalsoul
2009-10-25 18:49:16 |
this is the best way !
|
Plantis
2010-04-03 13:05:28 |
It is the best solution. It's so easy and represend all physics of this situation.
|
mvgnzls
2011-09-19 18:53:13 |
BEST SOLUTION!!!
|
walczyk
2011-11-11 10:29:40 |
This is pretty great. This problem is an uncommon example where energy is NOT the right/easy way to go about this, but dealing with force is. A particle whipping around a curve will sense a centripetal force IF it stays on the track. In this case the force of gravity is this centripetal force, at the highest point of the curve of course. g=a_c and the rest just falls right out. Great solution, this should be at the top, maybe if someone rewrites it.
|
|  | dannyboytward
2008-10-17 10:36:56 | Another solution:
Consider a reference frame moving at speed v. The particle only moves vertically. The surface is described by
d*cos[k(x-vt)]
The acceleration of the surface is the second time derivative
-d*(k*v)^2*cos[k(x-vt)]
which has maximum value of d*k^2*v^2. If this value is less than g, we have our answer. |  | Rus Almighty
2008-04-29 08:35:33 | A condition for the body to stay on the track:
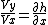
let's derive both sides by t and remember that on the top 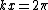 , Vx is V , , Vx is V , 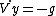 and and 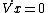 'cuase there is only gravitational force on the top. 'cuase there is only gravitational force on the top.
we get:
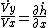
now let's calculate 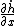
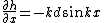
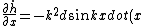 = - Vx k^2 d cos kx )
And from now on it's only algebra:
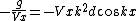
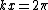
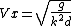
QED
Rus Almighty
2008-04-29 08:44:53 |
fix,
instead of 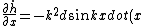 = - Vx k^2 d cos kx )
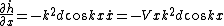
|
|  | panos85
2007-10-22 11:14:45 | Am I the only one thinking that it is more natural to let d go to 0 rather than infinity? If d=0, the particle will stay on track for any v, so (D).
elisa
2008-04-02 19:35:16 |
Great way to see it. The site is wonderful! Thank you everyone.
|
|  | emailzac
2007-10-08 10:47:34 | I'm pretty sure you can use limiting case here. If d gets very large, and k stays the same, the curve is going to be tighter, meaning the velocity's limit is going to decrease, therefore D is the only logical choice. |  | georgi
2007-08-30 22:53:17 | there is another great solution that is intuitive. in order for the particle to stay its velocity must be less than or equal to the phase velocity w/k of the wave. we are given k so we calculate w. w = sqrt(spring constant/m). recall F = spring constant * distance ==> mg = spring constant *d so spring constant = mg/d ==> w = sqrt(g/d) and voila your answer!
sawtooth
2007-10-29 10:40:17 |
I am sure this was one of the ways to solve the problem, that the guys at ETS wanted us to use. On the other hand, I am not conviced by your arguments georgi. It is not concise enough. I mean, for harmonic motion, you have to have a force that is propotional to the distance (or accelaration for that matter). 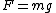 and we know and we know 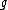 doesn't vary that much in small distances, and it is not that small to approximate its change as linear in distance. Furthermore, I think the frictionless surface demands a force vertical to the surface and the projection to the vertical axis has to have something to do with the vertical accelaration that has to be linear in distance. Something in the ways of skozmedia. I think there's another, similar, excercise in 8677 that uses chain rules and stuff. Anyway, I don;t have the time to write a complete answer, but even if it gives the right answer, I am not quite satisfied. Any thoughts? doesn't vary that much in small distances, and it is not that small to approximate its change as linear in distance. Furthermore, I think the frictionless surface demands a force vertical to the surface and the projection to the vertical axis has to have something to do with the vertical accelaration that has to be linear in distance. Something in the ways of skozmedia. I think there's another, similar, excercise in 8677 that uses chain rules and stuff. Anyway, I don;t have the time to write a complete answer, but even if it gives the right answer, I am not quite satisfied. Any thoughts?
|
p3ace
2008-07-26 15:23:37 |
The expression for h is the solution to the harmonic oscillator problem. That is why it is valid.
|
|  | skozmedia
2006-03-27 23:14:32 | Actually, there's a much more direct way. Use the fact that y(x)=-.5gt^2 and h(x)=-dcos(kx) along with x=vt. Substitute in, calculate dy/dx and dh/dx. You will need to use l'Hopital's rule for x=0, but that's easy.
Jeremy
2007-11-10 11:33:16 |
I just did something similar... Start by expanding ) about about 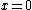 (the first hilltop): (the first hilltop): = d \cos (k x) \approx d-\frac{1}{2}d k^{2} x^{2}) . Now consider the path of a particle starting at the top of the hill with tangential velocity . Now consider the path of a particle starting at the top of the hill with tangential velocity  ; its position is given by two equations: ; its position is given by two equations: 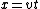 , and , and 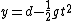 . For comparison with . For comparison with ) , combine the two previous equations to eliminate time: , combine the two previous equations to eliminate time: =d-\frac{1}{2}\frac{g}{v^{2}} x^{2}) . Thus, . Thus, 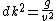 or or 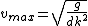 gives the maximal velocity. With this velocity, the particle follows the surface in freefall, e.g. if you were in a car going over the hill at this speed, you would experience weightlessness. At higher speeds, the particle will leave the surface. At lower speeds, the particle is kept at the surface via a normal force. The expansion about gives the maximal velocity. With this velocity, the particle follows the surface in freefall, e.g. if you were in a car going over the hill at this speed, you would experience weightlessness. At higher speeds, the particle will leave the surface. At lower speeds, the particle is kept at the surface via a normal force. The expansion about 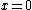 is justified because this is where the largest curvature is. (In fact, this is the same assumption used in the "rigorous" version of the official solution). is justified because this is where the largest curvature is. (In fact, this is the same assumption used in the "rigorous" version of the official solution).
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
