|
GR9677 #97
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }Probability Density Current }Probability Density Current
If one has forgotten the expression for the probability density current, then one needs not despair! If one remembers the vaguest definition of a ``probability current," one can solve this problem without the usage of the forgotten formula:
Recall that the probability current density J is the difference between incoming P(in) and outgoing P(out) probability densities. This is just the difference between the probability densities of a rightwards moving plane wave and a leftwards moving plane wave, since the probability density is related to the wave function by 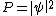
-P(out)=|f(e^{-i k x})|^2 - |f(e^{i k x})|^2)
The given wave function can be written in terms of plane waves,
 + \frac{\beta}{2i}(e^{ikx}-e^{-ikx}) \right)\\
&=&\left( (\alpha+\beta/i)\frac{e^{ikx}}{2} + (\alpha-\beta/i)\frac{e^{-ikx}}{2} \right)
\end{eqnarray})
) gives the coefficient for the leftwards (negative-direction) wave, while gives the coefficient for the leftwards (negative-direction) wave, while ) gives the coefficient for the rightwards traveling wave. The probability density for each wave is given by, gives the coefficient for the rightwards traveling wave. The probability density for each wave is given by,
|^2 &=& \frac{1}{4}\left(|\alpha|^2+|\beta|^2 + \frac{\alpha\beta^{*}}{-i} +\frac{\alpha^{*}\beta}{i}\right)\\
|f(e^{-ikx})|^2 &=& \frac{1}{4}\left(|\alpha|^2+|\beta|^2 + \frac{\alpha\beta^{*}}{i} -\frac{\alpha^{*}\beta}{i}\right)
\end{eqnarray})
Plugging these quantities into the formula for the probability current density above (J), one gets,
,) which is choice (E).
which is choice (E).
Alternatively:
The formal expression for the probability current density can be effortlessly derived from recalling the definition of probability and Schrodinger's Equation---both of which every physics (or engineering) major should know by heart.
Probability is defined (in the Born Interpretation) as |^2 dx) . One should recall that . One should recall that 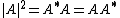 in general (to wit: the absolute value squared of a complex expression is itself times its complex conjugate). in general (to wit: the absolute value squared of a complex expression is itself times its complex conjugate).
The time-dependent Schrodinger's Equation is
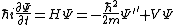 , ,
where 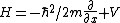 has the form of the familiar time-independent Hamiltonian. From this, one finds that has the form of the familiar time-independent Hamiltonian. From this, one finds that ) . .
Generalizing the idea of a current from classical physics to the idea of a probability current, one takes the time derivative of the probability to get dx) , where the product-rule for baby-math derivatives has been used and the derivative has been taken inside the integral because the integral and derivative are with respect to different variables. , where the product-rule for baby-math derivatives has been used and the derivative has been taken inside the integral because the integral and derivative are with respect to different variables.
Plugging in the expression for 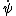 from the Schrodinger's Equation, one gets from the Schrodinger's Equation, one gets
+\Psi^* \frac{-i}{\hbar}\left( -\frac{\hbar^2}{2m}\Psi^{''}+V\Psi \right)\right)dx) , ,
where the terms involving V's cancel out, and thus,
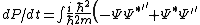dx = \frac{i\hbar}{2m}\int\left( -\Psi\Psi^{*''}+ \Psi^*\Psi^{''}\right)dx)
Rewriting dx = \int \frac{\partial}{\partial x} \left( -\Psi\Psi^{*'}+ \Psi^*\Psi^{'}\right)dx) , one can eliminate the integral in the probability current by applying the fundamental theorem of calculus (to wit: , one can eliminate the integral in the probability current by applying the fundamental theorem of calculus (to wit: -\psi(a)) ), ),
) . But, since the probability current is usually define as . But, since the probability current is usually define as -J(b)) , one has , one has
) . .
(Aside:) One can print-out a cool poster or decent T-shirt iron-on to remember the Schrodinger's Equation (among other miscellanai) at a site the current author made several years ago,
\begin{quote}
http://anequationisforever.com/ds.php
\end{quote}
One can remember the general form of the probability current by recalling that it has to do with the difference of 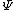 times its conjugate. times its conjugate.
Right, so onwards with the problem:
The problem gives the wave function, so one needs just chunk out the math to arrive at the final answer,
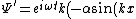 +\beta \cos(kx) \right))
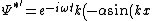 +\beta \cos(kx) \right))
Thus,
 +\beta^{*} \sin(kx) \right) \left( -\alpha \sin(kx) +\beta \cos(kx) \right)) and, and,
 +\beta \sin(kx) \right) \left( -\alpha^{*} \sin(kx) +\beta^{*} \cos(kx) \right)) , where one notes that the imaginary terms go to unity from the complex conjugate. , where one notes that the imaginary terms go to unity from the complex conjugate.
Plugging this into the probability current, one arrives at the expression for choice (E).
|
|
|
Alternate Solutions |
physics_guy
2018-08-15 02:45:41 | I think ETS really does want you to know the definition of current density. Otherwise, you should know that the probability current vanishes for nondegenerate stationary states, i.e. wavefunctions of the form (possibly time-dependent phase factor) x (real-valued function). In this problem, if we let a and b be real, then the probability current should vanish. Only choices A and E satisfy this, and choice A does seem suspiciously stringent. To see why A is false, let b = i * a. Then we have the wavefunction of a free particle of wavenumber k, whose probability current is not zero (even though its probability density is constant everywhere in space), but is instead equal to the probability density times the velocity of the the particle. |  | wavicle
2011-10-15 14:23:55 | Kudos on the  trick, but how do we KNOW that the PCD is not just zero for all values of trick, but how do we KNOW that the PCD is not just zero for all values of  and and  ? ?
It seems to me, that we can consider cos(kx) = 0 and calculate the PCD since the PCD should be valid for all values of kx. Then the PCD is
 = 0 \\ \Rightarrow \psi = \beta \\ \frac{d \psi}{dx} = -k\alpha \\ \psi \frac{d \psi*}{dx} - \frac{d \psi}{dx} \psi* = -k \beta \alpha* + k \alpha \beta*)
might be off by a sign, but who cares! |  |
|
|
Comments |
q
2019-10-16 00:55:56 | Bob Nightengale (BNightengale) Février 18, 2015The \'Los Angeles Times\' explique comment Rodriguez serait un ajustement parfait parce qu\'il ne peut statistiquement remplacer Jansen, et il en co?terait beaucoup moins que de négociation pour Jonathan Papelbon des Phillies de Philadelphie.\r\nq http://compu-technic.dk/tobuyen26.asp |  | physics_guy
2018-08-15 02:45:41 | I think ETS really does want you to know the definition of current density. Otherwise, you should know that the probability current vanishes for nondegenerate stationary states, i.e. wavefunctions of the form (possibly time-dependent phase factor) x (real-valued function). In this problem, if we let a and b be real, then the probability current should vanish. Only choices A and E satisfy this, and choice A does seem suspiciously stringent. To see why A is false, let b = i * a. Then we have the wavefunction of a free particle of wavenumber k, whose probability current is not zero (even though its probability density is constant everywhere in space), but is instead equal to the probability density times the velocity of the the particle.
physics_guy
2018-08-15 03:03:11 |
Alternatively, letting a or b = 0 gives you a particle-in-a-box stationary state times a phase factor. Since bound stationary states in 1-d are nondegenerate, the probability current must vanish. Again the only solutions that work are A and E, and A is not true in general.
|
|  | dragore
2012-08-16 11:58:34 | If by chance you can vaguely remember that:
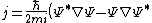)
Then all choices but (A) & (E) can be eliminated since (E) is the only one that has an imaginary unit in the denominator, as required. (A) sounds implausible given the freedom in the choice of  and and 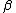 . .
QuantumCat
2014-09-18 14:51:32 |
I think because  and and 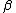 are given to be complex constants, E is the only correct answers, since A is a special case of E. When the imaginary components of are given to be complex constants, E is the only correct answers, since A is a special case of E. When the imaginary components of  and and 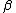 are zero we have A, however this is given not to be the case in the problem. are zero we have A, however this is given not to be the case in the problem.
|
|  | wavicle
2011-10-15 14:23:55 | Kudos on the 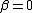 trick, but how do we KNOW that the PCD is not just zero for all values of trick, but how do we KNOW that the PCD is not just zero for all values of  and and 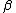 ? ?
It seems to me, that we can consider cos(kx) = 0 and calculate the PCD since the PCD should be valid for all values of kx. Then the PCD is
 = 0 \\ \Rightarrow \psi = \beta \\ \frac{d \psi}{dx} = -k\alpha \\ \psi \frac{d \psi*}{dx} - \frac{d \psi}{dx} \psi* = -k \beta \alpha* + k \alpha \beta*)
might be off by a sign, but who cares!
wavicle
2011-10-15 14:25:46 |
btw I don't bother with the 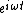 terms since they just "cancel" terms since they just "cancel"
|
|  | itorsics
2011-09-09 19:42:46 | Here's a quick heuristic way to derive the probability current.
If we assume the wavefunction 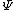 looks locally like a plane wave looks locally like a plane wave ) , then the "local value" of the velocity is , then the "local value" of the velocity is 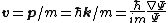 . The probability current is then . The probability current is then 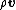 , where , where 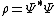 is the probability density. This gives is the probability density. This gives
) . However, this is not necessarily real, so we take the real part, which gives the standard formula for the probability current. . However, this is not necessarily real, so we take the real part, which gives the standard formula for the probability current. |  | scrabble
2011-03-22 07:50:55 | Note that the wave function can be reduced to that of a plane wave travelling in the +x or -x direction by setting 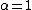 and and 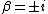 . In that case we should get either a positive or a negative probability current (either the particle is travelling to the left or to the right). The only answer that admits this change of sign is (E). . In that case we should get either a positive or a negative probability current (either the particle is travelling to the left or to the right). The only answer that admits this change of sign is (E). |  | The_Duck
2010-07-05 19:52:12 | Here's an instant solution if you can think of it: if alpha and beta are real (or if either equals zero, as ramparts mentioned), then I believe psi describes a stationary state and there should be no probability current. This immediately gives E, because C and D don't care whether alpha and beta are real or not (and A can't be right).
Another approach is to notice that if alpha = 1 and beta = i then you can simplify to the familiar form psi = exp(i[wt + kx]) which is a state with momentum eigenvalue -hbar*k. For a normalized momentum eigenstate like this I believe you can equate the probability current with the velocity, p/m = -hbar*k/m. Plugging these values of alpha and beta into the answers gives E.
Of course, I didn't think of either of these under time pressure. :/
flyboy621
2010-11-06 00:31:08 |
This has to be the way to do it.
If  or or 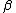 is zero, or if is zero, or if 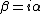 , we have a stationary state and the probability current must be zero. Otherwise the current must be nonzero. , we have a stationary state and the probability current must be zero. Otherwise the current must be nonzero.
(A) gives zero only if one of the coefficients actually is zero, so is not right in general. (B) doesn't depend on the coefficients at all, so can't be right. (C) gives zero only if BOTH coefficients are zero, which means there is no wave function at all. (D) would not give zero if only one coefficient is zero (though it would if 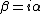 ), so it must be (E). ), so it must be (E).
|
physics_guy
2018-08-15 03:00:04 |
If b = i*a then you have the wavefunction of a free particle with wavevector k, which does have nonzero probability current. It is true that if a and b are real - or if a is any complex number and b is simply zero - then the probability current is zero. But it is not simply because psi is a stationary state. The condition for a state to be stationary is that the divergence of the probability current must vanish, not the probability current itself. However, if a stationary state is also nondegenerate, then the probability current vanishes. It is not clear that psi is a bound state here, indeed it looks more like a superposition of free particle wavefunctions, which are degenerate even in one dimension. However, if you are really itching for a shortcut, it follows from the definition of probability current that if psi is of the form (possibly time-dependent phase factor) x (real function of position) then the probability current vanishes. This is why letting a and b be real (or just letting b=0) gives you an instant solution. It\'s a nice trick for this problem, but I would argue it\'s hard to convince yourself it\'s true unless you knew the definition of J in the first place.
|
|  | ramparts
2009-10-02 12:11:54 | Oh, I think the probability current should go to 0 if 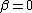 , no? That would only leave A and E (and A is just wrong ;) ). , no? That would only leave A and E (and A is just wrong ;) ).
niux
2009-11-04 19:23:14 |
nice
|
|  | ramparts
2009-10-02 12:10:48 | 1.8 minutes per problem.
I have yet to see a satisfactory answer to this problem for people who *don't* have the probability current memorized. |  | poop
2005-12-08 15:44:00 | Umm, I think there's an error in your sweet iron-on t-shirt. On the blackboard, doesn't the Schrodinger Equation have a second derivative in x, rather than a first derivative??
:-) |  | keflavich
2005-11-11 19:41:37 | That's a sweet 'effortless' derivation =P |  |
|
| Post A Comment! |
You are replying to:
I think ETS really does want you to know the definition of current density. Otherwise, you should know that the probability current vanishes for nondegenerate stationary states, i.e. wavefunctions of the form (possibly time-dependent phase factor) x (real-valued function). In this problem, if we let a and b be real, then the probability current should vanish. Only choices A and E satisfy this, and choice A does seem suspiciously stringent. To see why A is false, let b = i * a. Then we have the wavefunction of a free particle of wavenumber k, whose probability current is not zero (even though its probability density is constant everywhere in space), but is instead equal to the probability density times the velocity of the the particle.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
