|
GR0177 #86
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Copperknickers
2016-07-08 06:46:05 | Is there a simpler way to figure out the cos(wt), sin(wt) part? Without having to remember any formula by rote, that is? asdfman\'s solutions seems nice. Any alternative ones?
asdfasdfasdf
2016-09-07 14:53:11 |
I\'m not sure there\'s a simpler way to figure out the trig part. The only \"memorization\" needed is: (a) what are sin(0) and cos(0)? (b) what is the derivative of sin(wt) or cos(wt)? The question provides the initial condition of the n vector being parallel to the y-axis. When that is the case, there is no magnetic flux through the coil, right? So, when t=0, we should have B=0. sin(0)=0, so we\'ll use sine, not cosine. And you know you need to use some sort of periodic function since it\'s rotating...once it rotates such that the n vector lies parallel to the x-axis, we have the maximum flux possible, right? sin(90)=1, so that confirms that we should use sine.Then, since we get our emf from d(phi)/dt, we need the derivative of sin(wt), which is w*cos(wt).Does that help? [also, sorry if this text gets garbled...I\'m not sure why slashes are being randomly inserted.]
|
|  | John Smith
2013-10-17 02:02:09 | I am a foreigner, the time when I solve this question, I can hardly notice that the FUNK MILLIamperes. That will cost me lots of time if it happened in the real test. |  | asdfman
2009-11-02 23:47:03 | it says the coil starts at 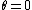 which means which means  = 0) and therefore a and therefore a 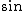 function. function.
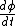 must therefore be a cosine. must therefore be a cosine.
Do some algebra and you realize that it'll be something like 1.5^2, so it'll have something ~2.25 or 2.5. The only answer that fits the bill is E. |  | theevilmachines
2009-07-12 17:58:53 | I don't know about you guys, but my 0177 test doesn't have ) as an answer choice. Choice E is as an answer choice. Choice E is ) . Am I missing something? . Am I missing something?
theevilmachines
2009-08-24 15:31:09 |
Oh it says in milliamperes, not amperes.
|
|  | duckduck_85
2008-11-03 22:20:12 | how do you know that the resistance given in the problem isn't for the entire coil? (so that you needn't take the # of turns into account)
elzoido238
2008-11-07 19:17:30 |
The problem states that "...the coil resistance is 9 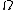 , which I interpret as the resistance of the entire coil. Since Yosun found the flux for 1 turn of the coil, you would need to account for the number of turns in the coil by dividing the total resistance by N (if, however one found the flux for the entire coil - i.e. , which I interpret as the resistance of the entire coil. Since Yosun found the flux for 1 turn of the coil, you would need to account for the number of turns in the coil by dividing the total resistance by N (if, however one found the flux for the entire coil - i.e. 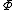 =NB =NB 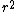 sin( sin(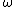 t) - one would not need to find the resistance per turn.) t) - one would not need to find the resistance per turn.)
Thanks Yosun for this kick-ass site! :)
|
|  | sblmstyl
2008-10-15 21:39:49 | thanks yosun! |  | naama99
2006-11-29 21:16:46 | What do you mean by \"one uses Ohm's Law in Faraday's Law"? Can you be more specific about it? It seems to me that you are taking the R given in the question and merely using it as L
Richard
2007-10-29 09:53:54 |
I'm pretty sure she just means,
take Ohm's law 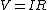 and substitute the expression for the induced voltage given by Faraday's law: and substitute the expression for the induced voltage given by Faraday's law:
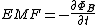
Of course you need to take into account the number of turns...
|
|  | radicaltyro
2006-10-28 21:53:31 | You are missing the  in your final answer. in your final answer. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
